stop-the-world

takuya-a のブログ

Information Retrieval and Web Search まとめ(13): 確率的情報検索(2) BM25

前回は、確率的情報検索の基本となる確率的ランキング原理とバイナリ独立モデルについて説明した。今回は確率的モデルによる重み付け手法である Okapi BM25 について解説する。

この記事は Information Retrieval and Web Search Advent Calendar 2020 の13日目の記事です。

adventar.org

ベクトル空間モデルの復習

  • クエリに含まれる単語が多く出てくる文書の順位は高くすべき
    • また、それは文書長などによって調整される
  • バイナリ独立モデル（BIM）ではだめなのか？
    • 初期の情報検索のモデルの多くは、タイトルや概要（長さがほぼ同じ）を対象にしており、全文検索はあまり意識されていなかった
    • ターム頻度を入れたモデルを作りたい
  • ベクトル空間モデル（復習）
    • クエリと文書を TF-IDF によって重み付けされたベクトルとして表現する
    • クエリベクトルと文書ベクトルのコサイン類似度スコアを計算
    • 文書をそのスコアによってランク付けする
    • 上位 K 件（例えば K = 10）をユーザに返す

Okapi BM25 の概要

  • Okapi BM25 は、検索システム Okapi を開発するなかで 25 番目に生まれた、タームの重み付け方法
  • BM25 は "Best Match 25" の意味
    • TREC で BM25 を採用するチームが増え始めた
    • 性能がよい
  • BM25 のゴール：パラメータを多く足さずに、ターム頻度や文書長をよく反映すること
    • [Robertson and Zaragoza 2009; Spärck Jones et al. 2000]
  • BM25 は文書の生成モデル
    • 単語（ターム）は多項分布 (multinominal distribution) から独立して生成されると仮定する

Poisson モデル

  • 文書のターム頻度の分布が、ポアソン分布で近似した二項分布に従う、と仮定するモデル
    • \lambda = Tp とすることで、二項分布をポアソン分布で近似できる
    • T は二項分布の試行回数、 p は試行の成功確率
  • Poisson モデルの問題点
    • ポアソン分布は（時間もしくは空間の）固定した区間内で事象が発生する回数をモデル化する
      • BM25 のモデルでは、文書から生成される単語がポアソン分布から発生していると仮定している
      • つまり、区間が固定されているというのは、文書長も固定されていることを意味している
      • これは後ほど修正する
    • 特定のトピックに関係する単語ではあまりフィットしない
      • 一般的な単語についてはよく当てはまる

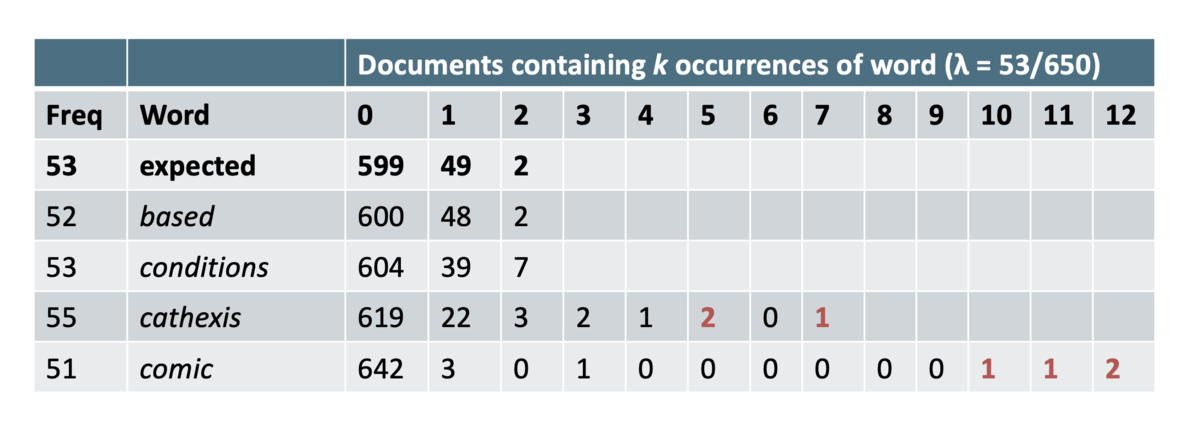
f:id:takuya-a:20201214042240p:plain
λ = 53/650 の単語についての、文書内の単語出現回数の分布。"cathexis"（医学用語？）や "comic" のような単語は、特定の文書に集中して出現している。 [Harter, “A Probabilistic Approach to Automatic Keyword Indexing”, JASIST, 1975]

エリートネス

  • ターム頻度をエリートネス (eliteness) という概念を使ってモデル化する
  • エリートネスとは、文書とタームの組における隠れ変数であり、ターム i に対して E_i と書くことにする
  • 文書中のタームについて、文書がある意味でそのタームで示される概念についての文書であるとき、そのタームはエリート (elite) であるという
    • エリートネスは2値で表現する（ E_i = elite or E_i = \overline{elite}）
  • NFL draft に関する Wikipedia 記事内の、エリートなタームの例（太字）を以下に示す

The National Football League Draft is an annual event in which the National Football League (NFL) teams select eligible college football players. It serves as the league’s most common source of player recruitment. The basic design of the draft is that each team is given a position in the draft order in reverse order relative to its record ...

  • タームの出現はエリートネスに依存する
  • エリートネスは適合度に依存する

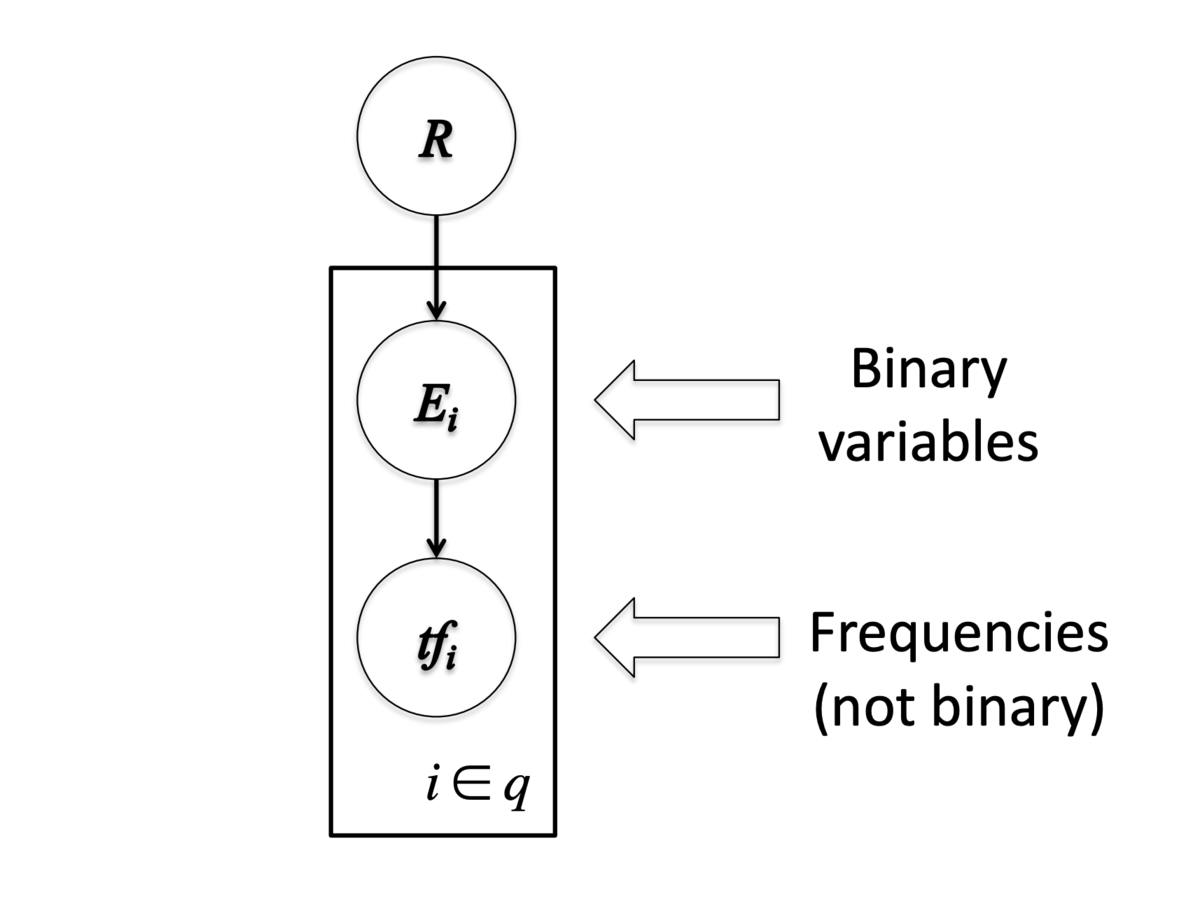
f:id:takuya-a:20201214042854p:plain
エリートネス（Ei）を追加したグラフィカルモデル

Poisson モデルの Retrieval Status Value

  • BIM のときと同様に、Retrieval Status Value (RSV) を考える

RSV^{elite} = \displaystyle\sum_{i \in q, tf_i > 0} c_i^{elite} (tf_i); \;
c_i^{elite} (tf_i) = \log \frac{ p( TF_i = tf_i \mid R=1 ) p( TF_i = 0 \mid R=0 ) }{ p( TF_i = 0 \mid R=1 ) p( TF_i = tf_i \mid R=0 ) }
  • エリートネスを使って p\left( TF_i = tf_i \mid R \right) は以下のように展開できる
\begin{eqnarray}
p\left( TF_i = tf_i \mid R \right)
&=& p(TF_i = tf_i \mid E_i = elite) p(E_i = elite \mid R) \\
&+& p(TF_i = tf_i \mid E_i = \overline{elite}) \left( 1 - p(E_i = elite \mid R) \right)
\end{eqnarray}

2-Poisson モデル

  • 前述した Poisson モデル（1-Poisson モデルと呼ぶ）の問題を解決するため、2つのポアソン分布でフィッティングする
  • 2-Poisson モデルでは、タームがエリートかどうかによって分布が変わる

p \left( TF_i = k_i \mid R \right) =
\pi \frac{\lambda^k}{k!} e^{-\lambda} +
(1 - \pi) \frac{\mu^k}{k!} e^{-\mu}
  • \pi は文書がタームに対してエリートである確率
  • \pi、 \lambda、 \mu の値はわからない

2-Poisson モデルの Retrieval Status Value

  • c_i^{elite} (tf_i) が満たすべき性質
    • c_i^{elite} (0) = 0
    • c_i^{elite} (tf_i) は tf_i によって単調に増加
    • tf_i \to \infty で最大値に漸近的に近づく
      • 単に tf をスケーリングするだけではこの性質を満たせない
    • 漸近的な極限は c_i^{BIM}
      • エリートネスの重み
  • 2-Poisson モデルのパラメータ（tex: \pi]、 \lambda、 \mu）を推定するのは容易ではない
  • --> 上記の性質を満たす、以下の飽和関数で近似する
 \dfrac{tf}{k_1 + tf}

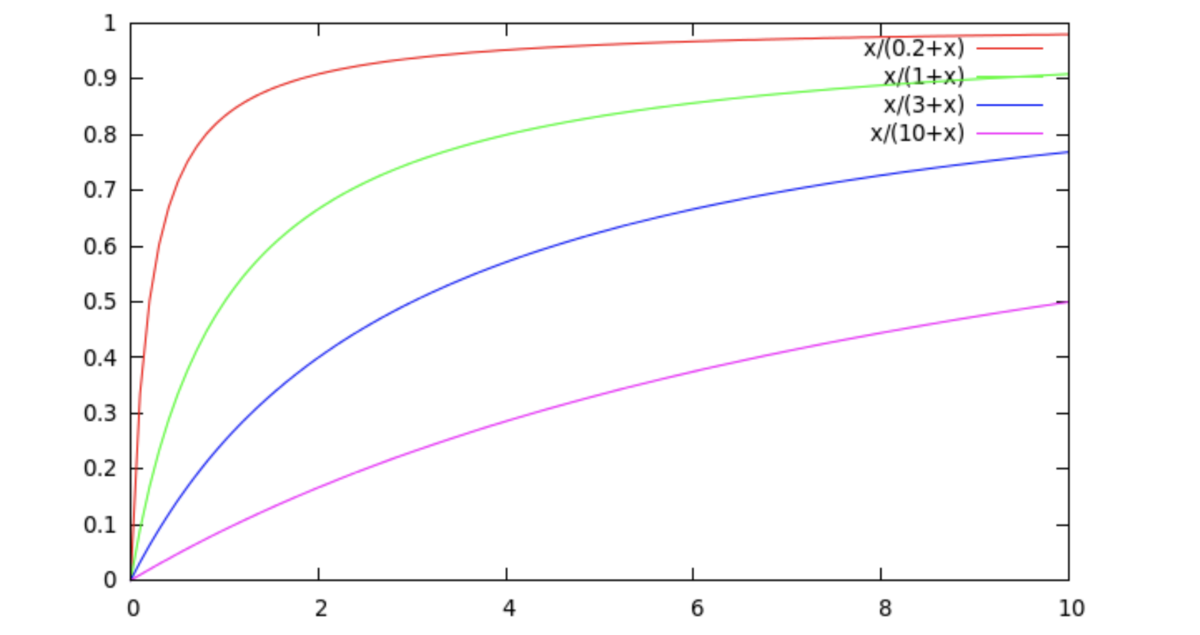
f:id:takuya-a:20201214142641p:plain

  • パラメータが1つしかなくシンプル
  • k_1 が大きいとき (例： k_1 = 10) でも tf_i はスコアにちゃんと寄与する
  • k_1 が小さいとき (例： k_1 = 0.2) には関数はすぐに飽和し、 tf_i からの寄与は小さくなっていく

Okapi BM25

BM25 の原形

  • Version 1
    • 上記の飽和関数をそのまま使ったバージョン
    • バイナリ独立モデル (BIM) に飽和関数をかませる
 c_i^{BM25v1} (tf_i) = c_i^{BIM} \dfrac{tf_i}{k_1 + tf_i}
  • Version 2
    • BIM を IDF に置き換えて簡略化
    • (k_1 + 1) は、ランキングを変化させずに tf_i = 1 のときにスコアを 1 にするための項
    • TF-IDF に似ているが、タームによるスコアは上限がある
 c_i^{BM25v2} (tf_i) = \log \dfrac{N}{df_i} \cdot \dfrac{(k_1 + 1) tf_i}{k_1 + tf_i}

文書長による正規化

  • 長い文書では tf_i が大きくなる傾向がある
  • 文書が長くなっている可能性
    • 冗長性：観測された tf_i が大きすぎる
    • 大きいスコープ：観測された tf_i は適正
  • 実際の文書では両方の影響がある
    • 部分的になんらかの正規化をする必要がある
  • 文書長 dl = \displaystyle\sum_{i \in V} tf_i
    • コレクションでの文書長の平均を avdl とする
  • 文書長の正規化を以下で行う
 B = \left( (1-b) + b \frac{dl}{avdl} \right), \; 0 \leq b \leq 1
  • 正規化の強さをパラメータ b で調整する
    • b = 1: 文書長で完全に正規化
    • b = 0: 文書長による正規化をしない

BM25

  • ターム頻度 tf_i を文書長で正規化する
    • tf_i' = \dfrac{tf_i}{B}
    • tf_i が元の tf、正規化後の tf が tf_i'
  • これを使って c_i^{BM25}(tf_i) を以下のようにする
\begin{eqnarray}
c_i^{BM25}(tf_i)
&=& \log \frac{N}{df_i} \cdot \frac{ (k_1 + 1) tf_i' }{ k_1 + tf_i' } \\
&=& \log \frac{N}{df_i} \cdot \frac{ (k_1 + 1) tf_i }{ k_1 \left( (1-b) + b \frac{dl}{avdl} \right) + tf_i }
\end{eqnarray}
  • よって、BM25 のランキング関数は
\begin{eqnarray}
RSV^{BM25}
&=&
\displaystyle\sum_{i \in q} c_i^{BM25}(tf_i) \\

&=&
\displaystyle\sum_{i \in q}
\log \frac{N}{df_i} \cdot
\frac{ (k_1 + 1) tf_i }{ k_1 \left( \left( 1-b \right) + b \frac{dl}{avdl} \right) + tf_i }
\end{eqnarray}
  • k_1 はターム頻度の寄与をスケーリングする
    • k_1 = 0 のときはバイナリモデルになり、 k_1 = 1 のときはターム頻度そのものを使うことになる
  • b は文書長の正規化の強さを調整する
    • b = 0 のときは正規化なし、 b = 1 のときは完全に文書長でスケーリングする（相対的なターム頻度を使う）
  • 典型的なパラメータ
    • k_1 は 1.2-2
    • b はおよそ 0.75
  • BM25 のほうがベクトル空間モデルの TF-IDF よりよくなる例
    • クエリが machine learning だったとする
    • 以下のような文書があったとする
      • 文書1: learning の tf が 1024、machine が 1
      • 文書2: learning の tf が 16、machine が 8
      • 文書2 のほうが適合度が高いと思われる
    • TF-IDF: \log_2 tf \cdot \log_2 (N/df)
      • 文書1: 11 * 7 + 1 * 10 = 87
      • 文書2: 5 * 7 + 4 * 10 = 75
    • BM25（ k_1 = 2 のとき）
      • 文書1: 7 * 3 + 10 * 1 = 31
      • 文書2: 7 * 2.67 + 10 * 2.4 = 42.7

講義資料

参考資料