stop-the-world

takuya-a のブログ

Information Retrieval and Web Search まとめ(21): リンク解析

前回はランク学習手法について説明した。今回は、リンク解析について扱う。

この記事は Information Retrieval and Web Search Advent Calendar 2020 の21日目の記事です。

adventar.org

リンク解析の概要

ハイパーテキストとリンク

  • 文書のコンテンツ以外のものもスコアリングに取り入れる
  • リンクは権威 (authority) をページに与えることを意味するのか？ランキングに役立てることはできるか？
    • CERN のホームページからリンクされたページは高エネルギー物理に関するページ？
  • 応用範囲
    • Web
    • Email
    • SNS

リンク解析と情報検索

  • スコアリングとランキング
  • リンクベースでのクラスタリング
    • トピックによる文書分類
  • リンクを分類の特徴量として使う
    • 同じ文書を指している文書たちは同じようなテーマである可能性が高い
  • クローリング
    • 次回扱う

有向グラフとしての Web

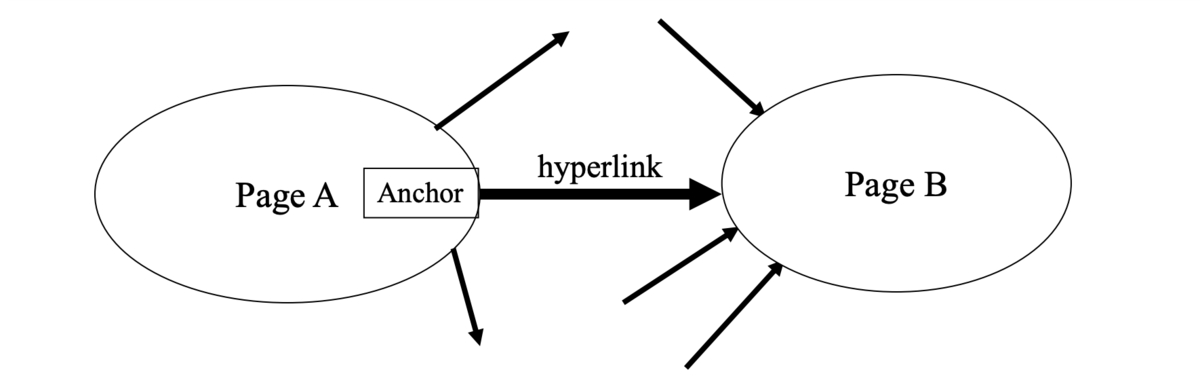
  • Web はページ内にアンカー (anchor) をもつ
  • Web はページを頂点、ハイパーリンクを辺とする有向グラフとみなせる

f:id:takuya-a:20201222234147p:plain
Web のグラフ構造

  • 仮説1
  • 仮説2
    • ページAのハイパーリンクのアンカーテキストには、リンク先のページBの内容が書かれている

PageRank

引用解析

  • 論文などの学術文献の引用関係を解析
  • 同じ文献を引用している文献同士は関連している
  • PageRank の基礎となった

学術文献と Web との違い

  • Web は数百万の書き手がいて、それぞれが違う興味を持っている
  • スパムが多い
  • 検索エンジンがリンクをランキングに使い始めると、リンクスパムが増える
    • お互いにリンクを張り合うリンクファーム (link farm) も存在する

PageRank スコアの基本的な考え方

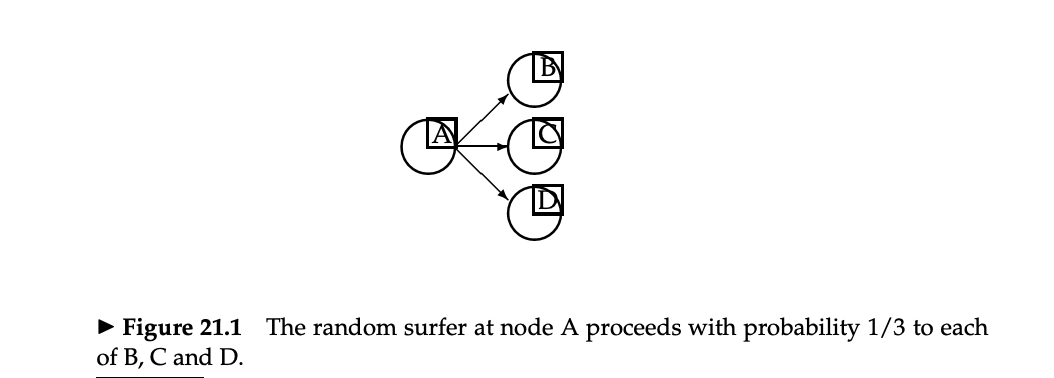
  • ユーザはページ間をランダムウォークすると仮定する
    • ランダムなページから開始
    • 各ステップで、ユーザはページから出ているリンクの中から等確率で1つ選んで遷移する
  • 長い時間のあと、各ページはある一定の訪問率 (vist rate) に落ち着く
    • これをそのページのスコアとする

f:id:takuya-a:20201222234252p:plain
(IIR p.464 Figure 21.1) ランダムウォークするユーザのページ遷移

テレポート

  • しかし、この方法には問題がある
    • dead-end （リンクを持たない Web ページ）がたくさんある
    • ランダムウォークを継続できない（スタック (stuck) する）
    • 訪問率が意味を持たなくなる
  • dead-end に行き当たったら、次はランダムなページに遷移する
    • スタックしなくなる
  • また、dead-end でないページでも、ある確率（たとえば 10%）の確率でランダムなページに遷移する
    • この確率は PageRank のパラメータであり、テレポート確率 (teleportation probability) と呼ぶ
    • Web のユーザがどこか他のページに行く挙動をシミュレートしている
  • すべてのページに訪問率が存在するようになる
    • この訪問率をどうやって計算するか？

マルコフ連鎖

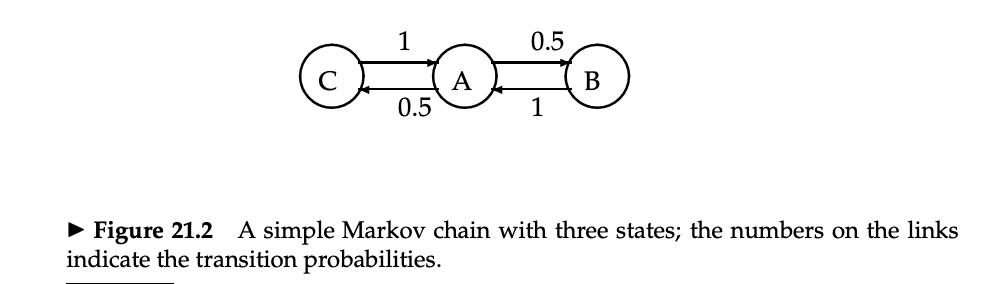
  • マルコフ連鎖 (Markov chain) は n 個の状態 (state) と、 n×n の遷移確率行列 (transition probability matrix) P からなる
  • 各ステップで、状態のうちのどれか1つの中にいる
  • P_{ij} は、状態 i から状態 j へ遷移する確率を表す
    • P_{ii} > 0 も認められる
  • すべての i に対して
 \displaystyle\sum_{j=1}^{n} P_{ij} = 1

マルコフ連鎖の例

f:id:takuya-a:20201222234405p:plain
(IIR p.466 Figure 21.2) マルコフ連鎖の例


P = \left(
  \begin{array}{ccc}
    0 & 0.5 & 0.5 \\
    1 & 0   & 0   \\
    1 & 0   & 0
  \end{array}
\right)

エルゴード的マルコフ連鎖

  • エルゴード的マルコフ連鎖 (ergodic Markov chain) は、各状態での長期的な訪問率がユニーク（一意）である
    • エルゴード的：周期的なパターンがない
    • テレポートによりエルゴード性が満たされる
  • 長期的には、この訪問率に比例して各状態に遷移する
  • どこから開始するかには依存しない

確率ベクトル

  • 確率（行）ベクトル x = (x_1, ..., x_n) は、どの状態にいるかを示す
    • (0, 0, ..., 0, 1, 0, ..., 0) （i 番目の要素だけ 1）のとき、状態 i にいる
    • より一般には、確率ベクトル x = (x_1, ..., x_n) は、状態 i にいる確率 x_i を意味する
 \displaystyle\sum_{i=1}^n x_i = 1
  • このステップでの確率ベクトルが x = (x_1, ..., x_n) だったとき、次のステップはどうなるか？
  • 行列 P が、状態 i からの遷移確率を示していることを思い出すと、次の状態は xP と表せる
    • その次は xP^{2} 、更にその次は xP^{3}...
    • これは収束するか？
    • これを計算して調べるのがべき乗法 (power method, power iteration)
      • 初歩的な方法
      • 訪問頻度が一定の閾値以下に「落ち着く」までシミュレートを繰り返す
  • 確率行ベクトルの定常状態を a = (a_1, ..., a_n) と書くことにする
    • これは定常状態なので、 a = aP
  • この方程式を解くと a を求めることができる

Web グラフの例

f:id:takuya-a:20201223005928p:plain
6つのページ（状態）をもつ小さい Web のグラフと、その遷移確率行列

  • dead-end (sink) となるページ（状態 2）からは、ランダムなページに遷移するように修正する

f:id:takuya-a:20201223010257p:plain
dead-end を修正した遷移確率行列

  • テレポートの効果を入れる

f:id:takuya-a:20201223010043p:plain
テレポートによるランダムな遷移を追加した遷移確率行列

f:id:takuya-a:20201223010122p:plain
べき乗法で計算した確率ベクトル。収束していく様子が見える

HITS

講義資料

参考資料