stop-the-world

takuya-a のブログ

Information Retrieval and Web Search まとめ(20): ランク学習

前回は Word2vec, BERT などの単語埋め込み手法と、それらの情報検索への応用について説明した。今回は、ランク学習について紹介する。

この記事は Information Retrieval and Web Search Advent Calendar 2020 の20日目の記事です。

adventar.org

情報検索のための機械学習

  • これまでに検索における文書のランキング手法をいくつか見てきた
    • コサイン類似度、BM25...
  • また、教師ありの機械学習を使った文書分類（クラス分類）の方法も見てきた
    • ロッキオの方法、kNN、決定木...
  • 文書のランク付けにも機械学習を使えないか？
    • "machine-learned releance", "learning to rank" として知られている

歴史

  • 検索ランキングのための機械学習はアクティブに研究されてきた
  • 過去の研究
    • Wong, S.K. et al. 1988. Linear structure in information retrieval. SIGIR 1988.
    • Fuhr, N. 1992. Probabilistic methods in information retrieval. Computer Journal.
    • Gey, F. C. 1994. Inferring probability of relevance using the method of logistic regression. SIGIR 1994.
    • Herbrich, R. et al. 2000. Large Margin Rank Boundaries for Ordinal Regression. Advances in Large Margin Classifiers.
  • 初期の研究はそれほどうまくいっていなかった
    • 訓練データが少なかった
      • 特に実世界のデータ
      • クエリログ、適合性判定のデータを集めるのは大変
    • 機械学習手法もまだ発展していなかった
    • 情報検索の問題への適用が不十分だった
    • 特徴量が十分ではなかった

機械学習の必要性

  • 現代的な（Web の）システムは大量の特徴量を扱う
    • ターム頻度などの古典的な特徴量だけではなく、ページ中の画像の数、リンクの数、PageRank、URL、更新日時、ページの表示速度...
  • Google は 2008 年には 200 以上の特徴量（シグナル）を使っており、今日では 500 以上になっているだろう

ランク学習

  • クラス分類はアドホック検索への適切なアプローチではない
    • クラス分類 (classification)：順序がないクラスへのマッピングを行う
    • 回帰 (regression)：実数へのマッピングを行う
    • 順序付き回帰 (ordinal regression)、あるいはランキング (ranking)：順序付きのクラスへのマッピングを行う
  • ランキング問題では、文書が他の文書に対してよいかどうかを議論する
    • よさの絶対的な尺度は必要ない
  • ランク学習 (learning to rank)
    • 以下のような適合性のカテゴリの集合 C が存在すると仮定する
      • C のすべてのカテゴリ c_i には全順序がついている (totally ordered)
        • c_1 \gt c_2 \gt ... \gt c_J
      • （これは順序付き回帰の問題設定と同じ）
    • 以下のような文書とクエリのペア (d, q) からなる訓練データを仮定する
      • (d, q) は特徴量ベクトル x_i で表され、それに適合ランキング c_i がついている

検索ランキングのためのアルゴリズム

  • SVM (Vapnik 1995) のランキングへの適用：Ranking SVM (Joachims 2002)
  • ニューラルネット：RankNet (Burges et al. 2006)
  • Tree Ensemble
    • ランダムフォレスト (Breiman and Schapire 2001)
    • Boosted Decision Tree
      • Multiple Additive Regression Trees (Friedman, 1999)
      • Gradient-boosted decision trees: LambdaMART (Burges, 2010)
      • AltaVista, Yahoo!, Bing, Yandex などの検索エンジンで採用事例あり
    • 2010 年の Yahoo! Learning to Rank Challenge ではすべてのトップチームが Tree Ensemle の手法の組み合わせを使った

Yahoo! Learning to Rank Challenge

回帰木

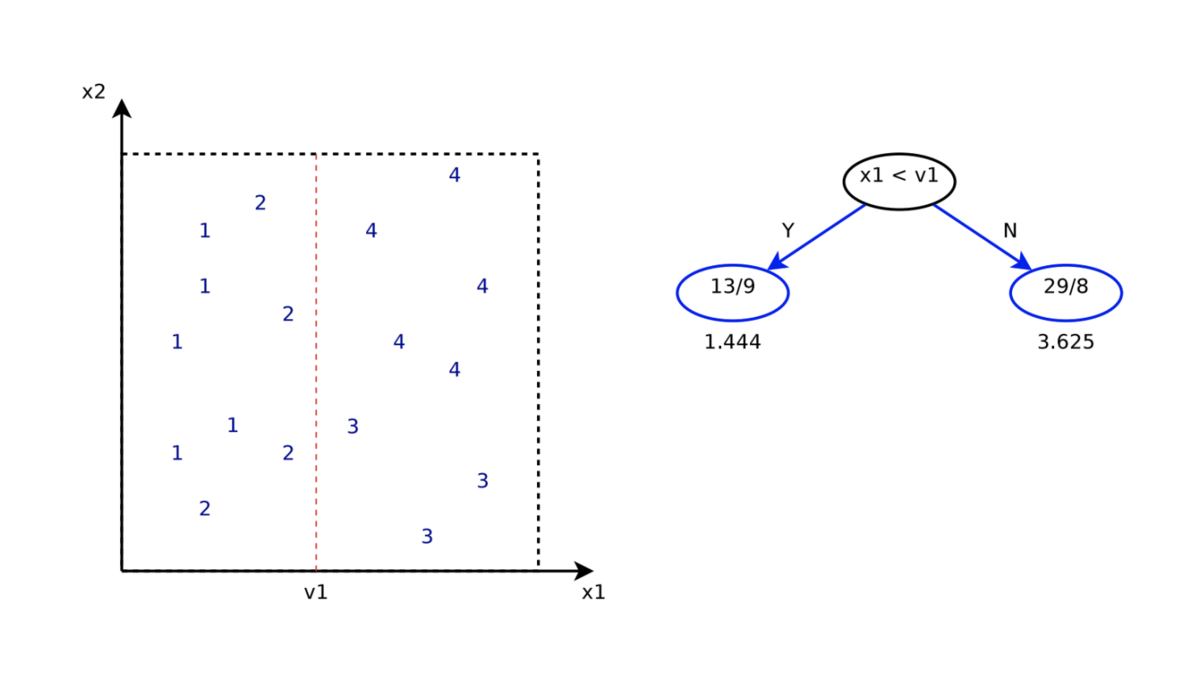
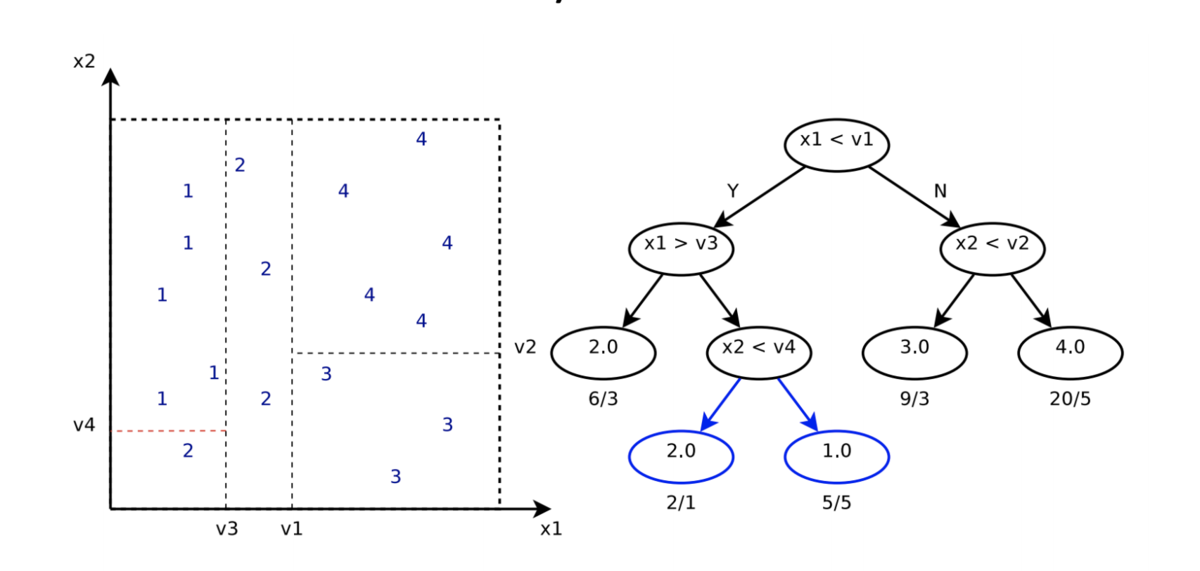
  • 回帰木 (regression tree) は、実数を予測できる決定木
  • 葉ノードには、その葉ノードに含まれるすべてのサンプルの平均値 (mean) を保持する
    • \gamma_{k} = f(x_i) = \overline{x_i}
  • 分割規準：標準偏差 (standard deviation; SD) の最小化
    • 値の分散（標準偏差 SD）を最小化するように分割 A を選択する
    • 標準偏差、サンプル数、もしくは木の深さのいずれかが閾値を下回ったら分割を止める
  • 学習時には、分割する変数 x_1 と、その変数上での分割点 v_1 を探索する
    • それらは予測誤差 \displaystyle\sum_{i} \left( y_i - f(x_i) \right) ^2 を最小化するように選ぶ

f:id:takuya-a:20201222053301p:plain
回帰木の分割の例(1)。予測誤差を最小化する分割を選択

f:id:takuya-a:20201222053337p:plain
回帰木の分割の例(2)。予測誤差が0になるまで分割を進めた

勾配ブースティング

ブースティングのモチベーション

  • Q:「独立な弱い (weak) 分類器を組み合わせて、高い精度の分類器を構築できるか？」
  • 古典的なアプローチ: AdaBoost
  • すべての木の重み付きの投票で分類する

ブースティングによる関数の推定

  • ほしいもの：損失関数 L(y, F(x)) の期待値を最小化する、以下のような関数 F^*(x)
 F^*(x) = \text{argmin}_{F(x)} \mathbb{E}_{y,x} L(y, F(x))
  • ブースティングでは、 F^*(x) を以下のような形で近似する
    • h(x; a) は a = { a_1, a_2, ..., a_n } でパラメータ化された関数
    • \beta は重み係数
 F(x) = \displaystyle\sum_{m=1}^M \beta_m h(x; a_m)

勾配ブースティングの学習

  • 勾配ブースティング (gradient boosting) は、任意の微分可能な損失関数に対して関数 F(x) を推定できる
  • 関数 h(x; a) を最小二乗法でフィッティングする
 a_m = \text{argmin}_a \sum_i [ \tilde{y_{im}} - h(x_i, a) ]^2
  • ただし \tilde{y_{im}} は「疑似残差 (pseudo-residual)」であり
 \tilde{y_{im}} = - \left[ \dfrac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]_{F(x) = F_{m-1}(x)}
  • 勾配ブースティングは、どんな損失関数であっても最小二乗法に単純化する

Gradient Boosted Regression Tree (GBRT)

  • Gradient Boosted Regression Tree (GBRT) は、この勾配ブースティングのアプローチを回帰木 (regression tree) に適用する
    • それぞれの回帰木は通常 1-8 の分割しか持たない
  • GBRT の学習
    • 最初に、すべての x_i に対して定数をとる、最もシンプルな予測器を学習する（[tex: F_0(x)）
      • 訓練データの誤差を最小化する定数
    • 木のルートノードの値 \gamma_{km} を探索する
    • 最小二乗法によりルートノードを分割する
    • さらに誤差を最小化する木を追加する

MART

f:id:takuya-a:20201222063819p:plain
MART の学習アルゴリズム

RankNet

  • RankNet [Burges et al. 2005] はニューラルネットによる ranker
  • モデルパラメータ w に対して微分可能な関数 f(x; w) をスコア関数とする
    • f(x_i; w) = s_i が x_i のスコア
  • クエリ q に対して、各文書の組 (d_i, d_j) に対するランキングのクラスの確率 P_{ij} を学習する
    • P_{ij} は、文書 d_i が d_j よりランキングが上である確率
    • \sigma はシグモイド関数の傾きを決めるパラメータ
 P_{ij} = P \left( d_i \succ d_j \right) = \dfrac{1}{1 + e^{-\sigma (s_i - s_j)}}
  • 損失関数 C はクロスエントロピー損失
    • P_{ij} はモデルの確率
    • \overline{P_ij} は実際の確率（各カテゴリに対して0/1で与えられる適合性の判定）
\begin{eqnarray}
C &=& - \overline{P_{ij}} \log P_{ij} - (1 - \overline{P_ij}) \log (1 - P_ij) \\
  &=& \frac{1}{2} (1 - S_{ij}) \sigma (s_i - s_j) + \log (1 + e^{-\sigma (s_i - s_j)})
\end{eqnarray}
  • ただし、 S_{ij} \in { 0, +1, -1 }
    • d_i が d_j よりも適合しているとき S_{ij} = 1
    • d_j が d_i よりも適合しているとき S_{ij} = -1
    • d_i と d_j が同じラベルのとき S_{ij} = 0

RankNet の Lambda

 \dfrac{\partial C}{\partial s_i} = \sigma \left( \dfrac{1}{2} (1 - S_{ij}) - \dfrac{1}{1 + e^{\sigma (s_i - s_j)}} \right) = - \dfrac{\partial C}{\partial s_j}
  • これを使って損失関数の w_k に対する微分は以下のようにできる
\begin{eqnarray}
\dfrac{\partial C}{\partial w_k} &=& \dfrac{\partial C}{\partial s_i} \dfrac{\partial s_i}{\partial w_k} + \dfrac{\partial C}{\partial s_j} \dfrac{\partial s_j}{\partial w_k} \\
&=& \sigma \left( \dfrac{1}{2} (1 - S_{ij}) - \dfrac{1}{1 + e^{\sigma (s_i - s_j)}} \right) \left( \dfrac{\partial s_i}{\partial w_k} - \dfrac{\partial s_j}{\partial w_k} \right) \\
&=& \lambda_{ij} \left( \dfrac{\partial s_i}{\partial w_k} - \dfrac{\partial s_j}{\partial w_k} \right)
\end{eqnarray}
  • この式を使って重み w_k を更新できる
  • \lambda_{ij} は、文書 d_i と d_j の組に対しての、変更したいスコアを表している
  • クエリ-文書ベクトル x_i の \lambda_{ij} と
    • \lambda_{ji} の総和 \lambda_i を定義する
 \lambda_i = \displaystyle\sum_{j:\{i,j\} \in I} \lambda_{ij} - \displaystyle\sum_{k:\{k,i\} \in I} \lambda_{ki}
  • この \lambda_i は、クエリ-文書ベクトル x_i のペアワイズ損失の勾配を表している
    • (a) は最適なランキング
    • (b) は 10 のペアワイズ誤差をもつランキング
    • (c) は 8 のペアワイズ誤差をもつ
    • 青の矢印は最後の文書の勾配 \lambda_i

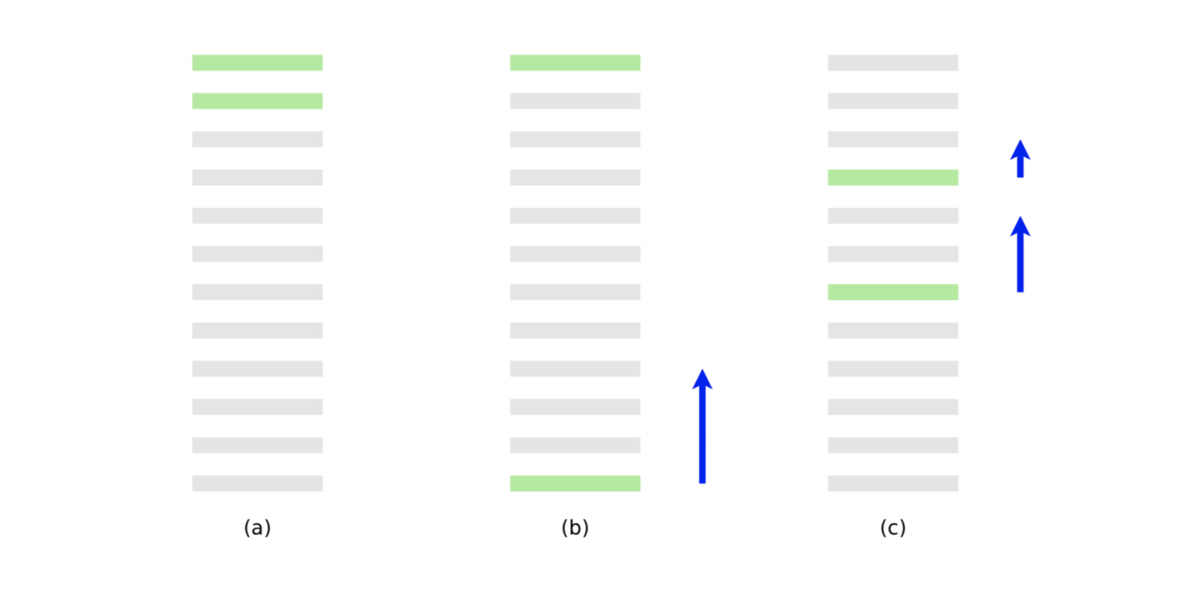
f:id:takuya-a:20201222153814p:plain
ランキングの損失とそれらの λi の例(1)

  • 青の矢印でペアワイズ誤差は減り、2値の適合性評価指標は改善する
  • しかし、NDCG や ERR のような、上位により大きい重みをつける指標では、以下の赤の矢印のような勾配のほうが望ましい

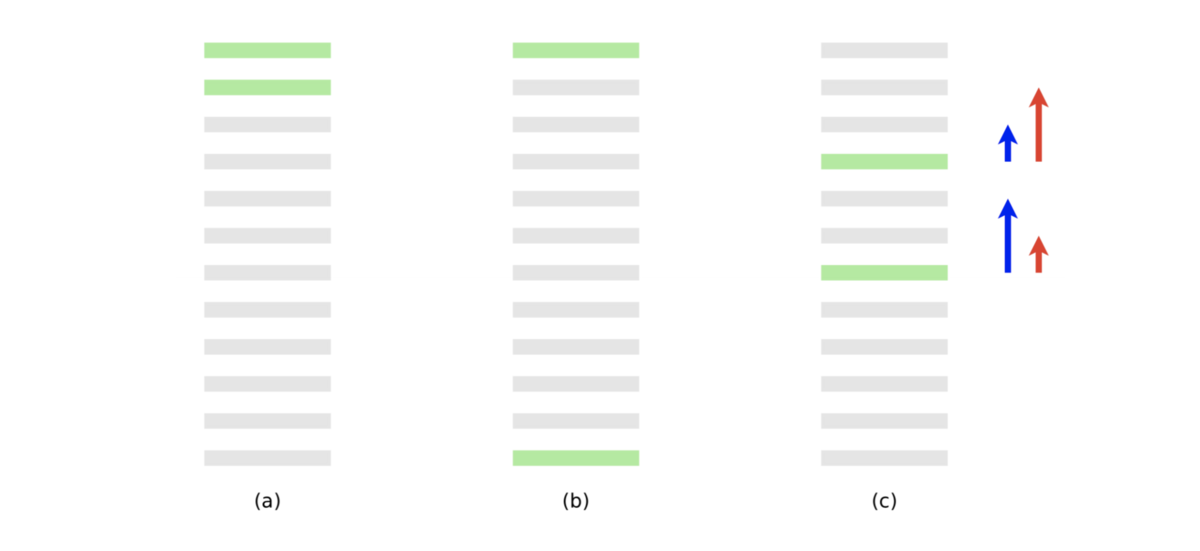
f:id:takuya-a:20201222153851p:plain
ランキングの損失とそれらの λi の例(2)

LambdaRank

  • LambdaRank [Burges et al. 2006]
  • RankNet のようなペアワイズ誤差ではなく、NDCG の効果を入れる
  • アイデア： lambda を | \Delta Z| 倍する
    • |\Delta Z| は、文書 d_i と d_j を交換したときの差分
  • |\Delta Z| として |\Delta NDCG| （NDCG の変化）を使って \lambda を以下のようにする
 \lambda_{ij} = \dfrac{\partial C (s_i - s_j)}{\partial s_i} = \dfrac{- \sigma}{1 + e^{\sigma (s_i - s_j)}} |\Delta NDCG|
  • Burges et al. は、この変更によって NDCG に対して十分に最適化できることを示した

LambdaMART

  • LambdaRank は勾配をモデル化している
  • MART は勾配（勾配ブースティング）によって学習できる
  • この2つを組み合わせたのが LambdaMART [Burges 2010]
    • MART に LambdaRank の勾配を入れた

f:id:takuya-a:20201221041428p:plain
([Burges 2010] Algorithm: LambdaMART) LambdaMART のアルゴリズム

  • 前述の通り、Yahoo! Learning to Rank Challenge で LambdaMART （と他のモデルとの線形結合）を使ったチームが優勝 [Burges et al. 2011]
  • 結合されたモデルと、それぞれの単体でのスコアは以下の通り

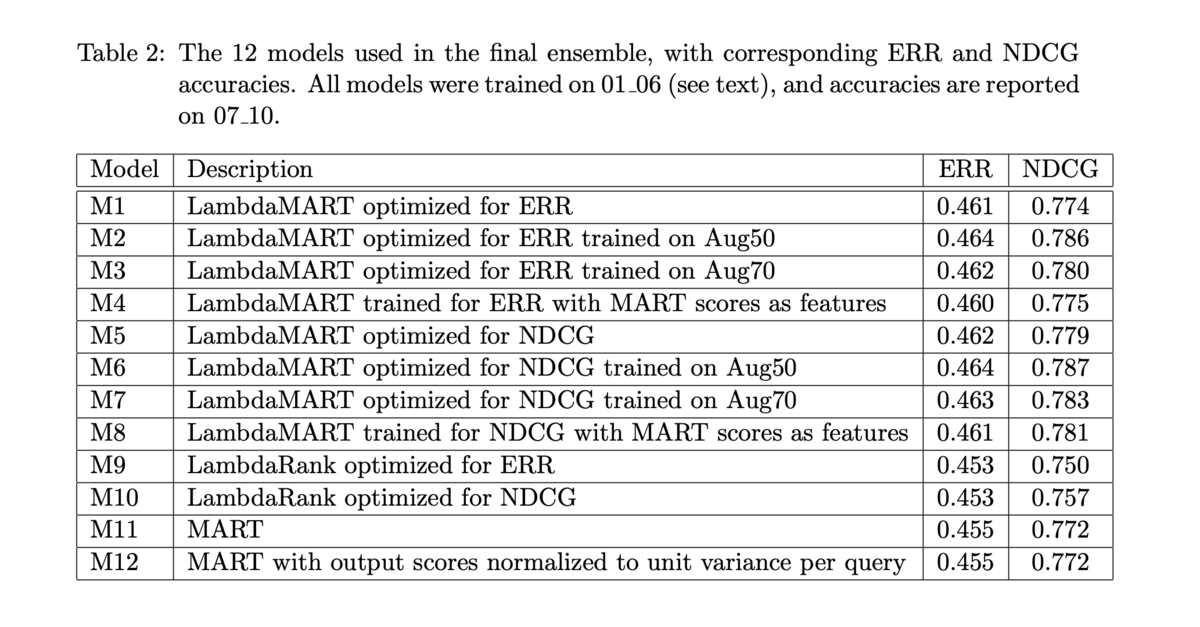
f:id:takuya-a:20201222164100p:plain
([Burges et al. 2011 Table 2]) 使用されたモデルと単体でのスコア

  • 多くのモデルを組み合わせなくても十分に高い性能を示す

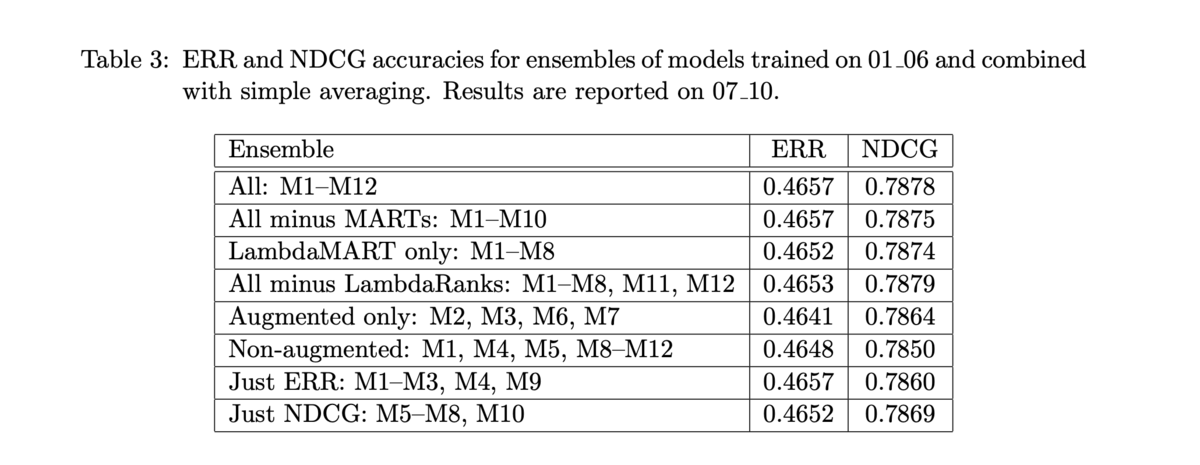
f:id:takuya-a:20201222164143p:plain
([Burges et al. 2011 Table 3]) モデルの組み合わせとそれぞれのスコア

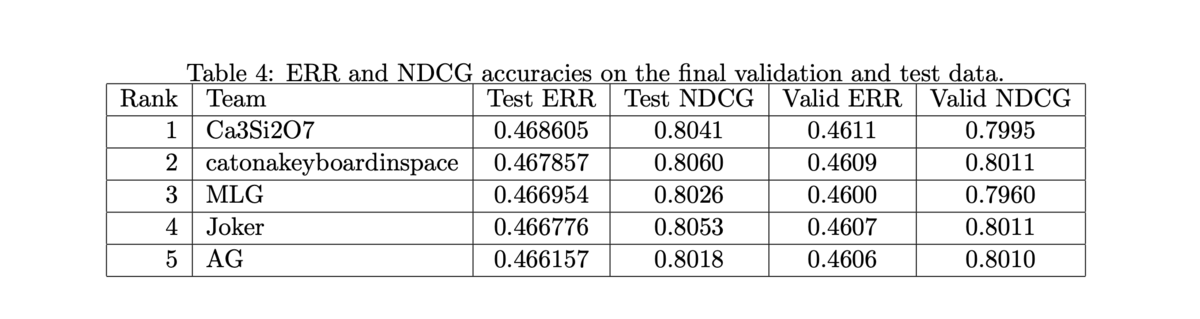
  • 他のチームも僅差
    • ペアワイズの Logistic Rank もいい結果を残している

f:id:takuya-a:20201222164220p:plain
([Burges et al. 2011 Table 4]) Yahoo! Learning to Rank Challenge の最終スコア。1位のチームが LambdaMART

  • だが、決定木ベースの手法は検索エンジンの会社では必要不可欠になっているようだ

講義資料

参考資料